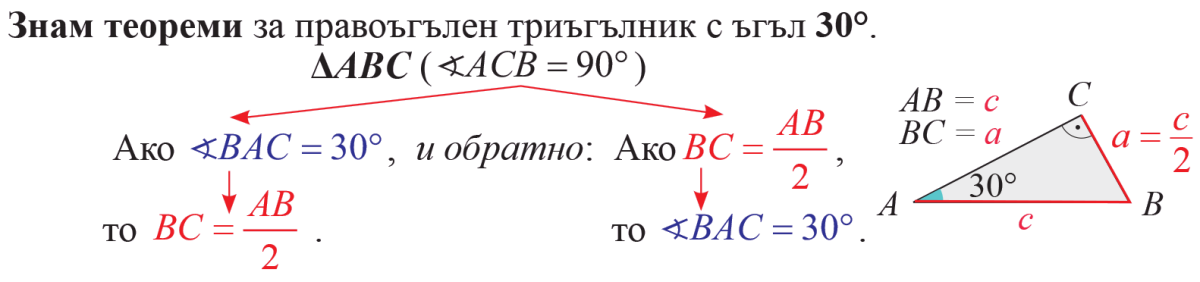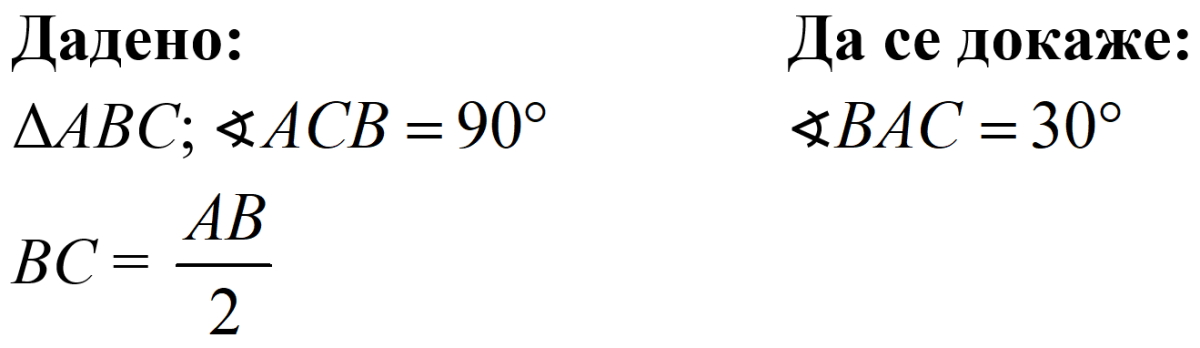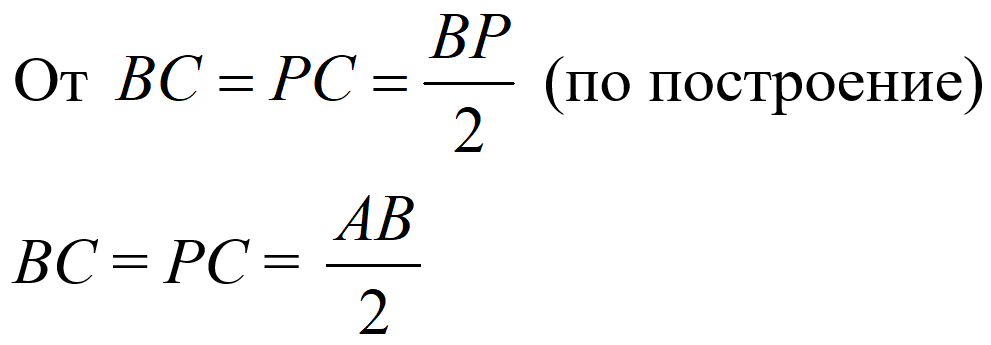Правоъгълен триъгълник
с ъгъл 30°
В този урок ще научите:
- теорема за катета, лежащ срещу ъгъл 30° в правоъгълен триъгълник;
- да използвате теоремата за решаване на задачи;
- обратната теорема за ъгъл в правоъгълен триъгълник, лежащ срещу катет, който е два пъти по-малък от хипотенузата му;
- да използвате обратната теорема за решаване на задачи.
Знаете ли, че
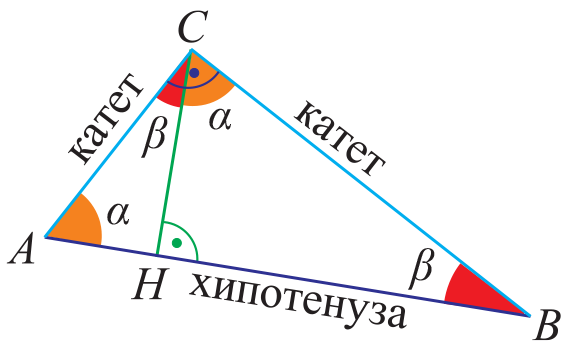
Думите „катет“ и „хипотенуза“ имат гръцки произход.
„Катет“ означава „спуснат отвес“ или перпендикуляр.
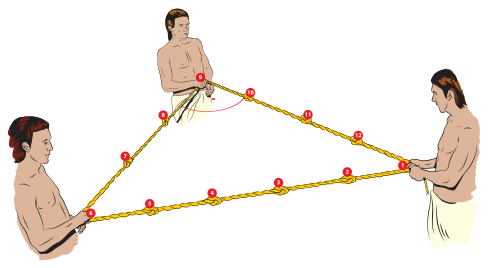
Думата „хипотенуза“ произхожда от начина на построяване на египетски триъгълници с помощта на опънато въже. Евклид я нарича „страна, която стяга правия ъгъл“.
Даден е правоъгълен ∆ABC
с хипотенуза AB и остри ъгли α и β.
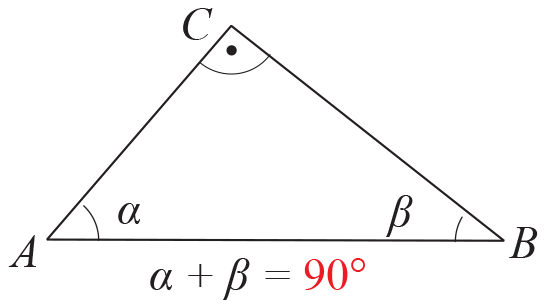
Ако α = 70°, то β = 90° – 70° = 20°.
Ако α = 2β°, то β = 30° и α = 60°.
Ако α : β = 4 : 5, то α = 40° и β = 50°.
Ако ∆ABC e равнобедрен, то α = 45° и β = 45°.
Правоъгълен триъгълник с ъгъл 30°
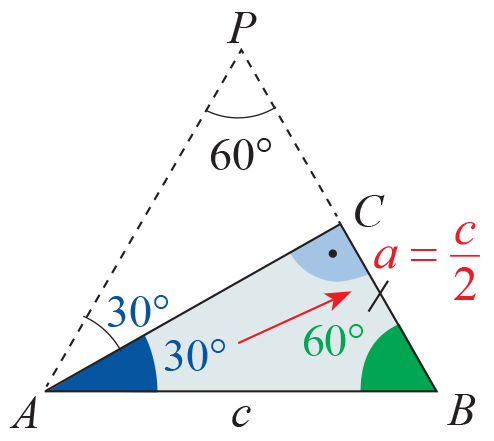
Теорема 1 Катетът, лежащ срещу ъгъл от 30° в правоъгълен триъгълник, е равен на половината от хипотенузата.
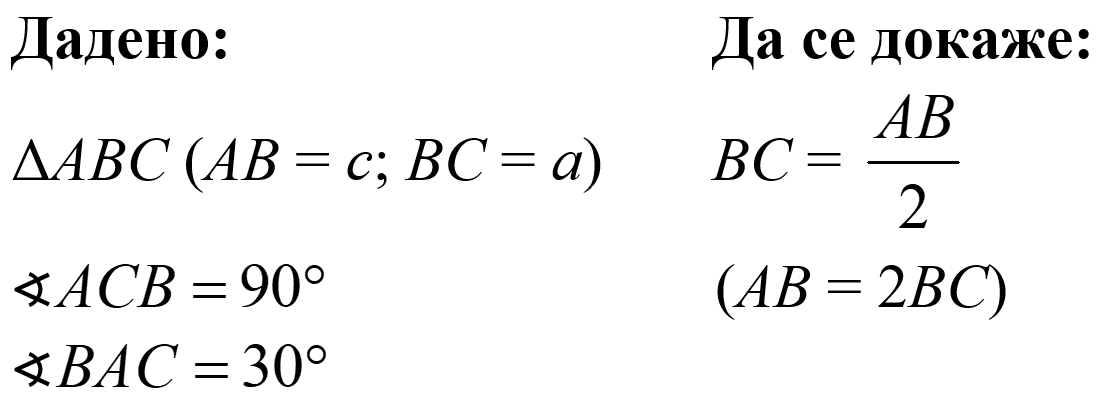
Доказателство:
Върху лъча BC построяваме отсечка CP = BC.
Разглеждаме ∆ABC и ∆APC.
1. BC = PC по построение
2. AC – обща
3. ∢ACB = ∢ACP = 90°
⇒ ΔABC ≅ ΔAPC по първи признак ⇒ AB = AP и ∢BAC = ∢PAC = 30° (съответни елементи) ⇒ ∢BAP = 60° ⇒ ΔABP е равностранен ⇒ BP = AB
⇒ ΔABC ≅ ΔAPC по първи признак ⇒ AB = AP и ∢BAC = ∢PAC = 30° (съответни елементи) ⇒ ∢BAP = 60° ⇒ ΔABP е равностранен ⇒ BP = AB
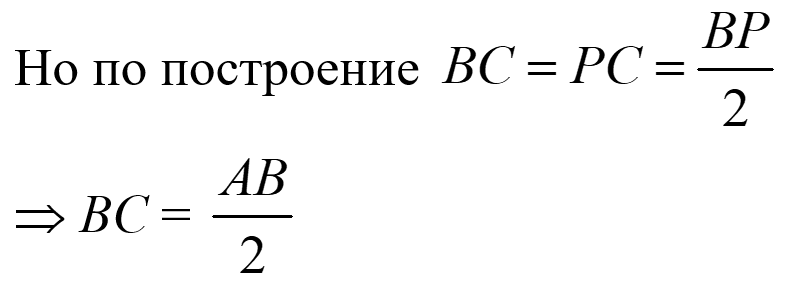
По данните на чертежа намерете дължината
на страната, означена с x.
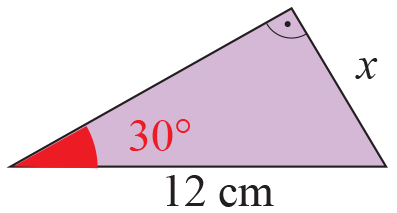

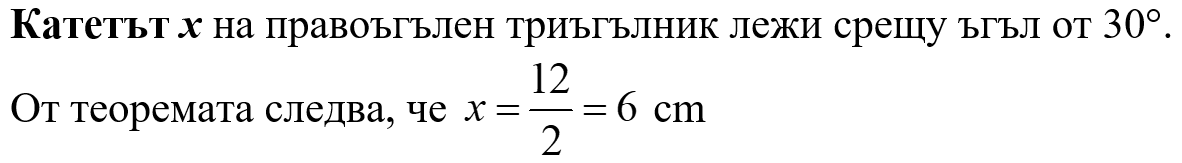
По данните на чертежа намерете дължината на страната, означена с x.
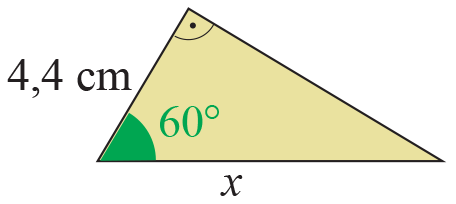

Даден е правоъгълен триъгълник с хипотенуза x и остър ъгъл 60°. Следователно другият му остър ъгъл е 30°.
Катетът, който лежи срещу ъгъла от 30°, е равен на 4,4 cm.
От теоремата следва, че хипотенузата x = 2 . 4,4 = 8,8 cm.
По данните на чертежа намерете дължината
на страната, означена с x.


Даден е правоъгълен триъгълник с хипотенуза, равна на (x + 3) cm. Катетът, който е равен на x cm, лежи срещу ъгъл от 30°.
От теоремата следва, че x + 3 = 2x.
Следователно x = 3 cm
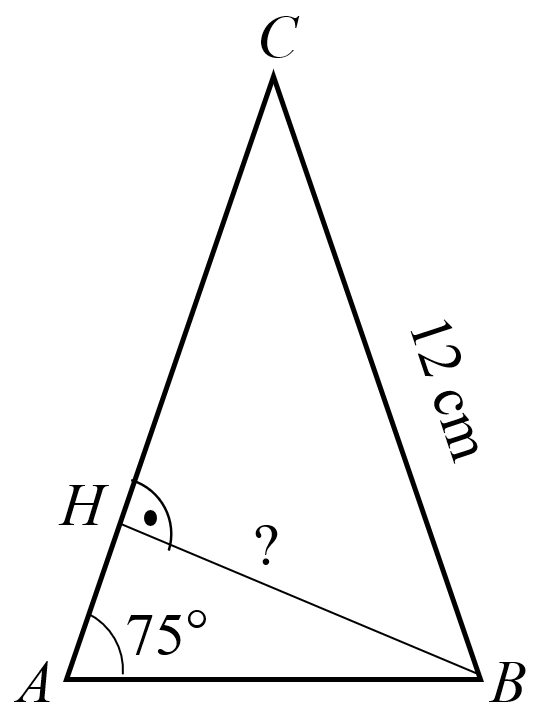
На чертежа ∆ABC е равнобедрен с бедра AC = BC = 12 cm и ∢BAC = 75°. Намерете дължината на височината BH.

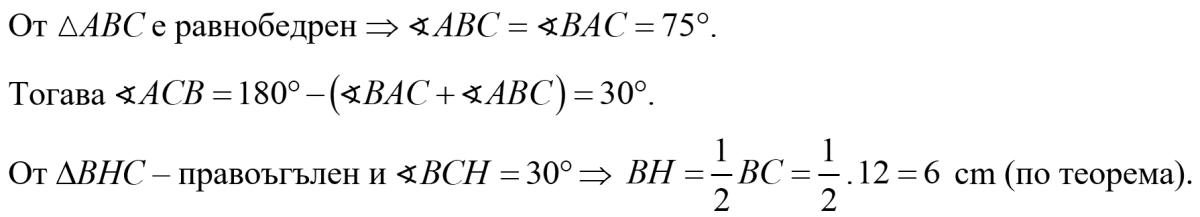
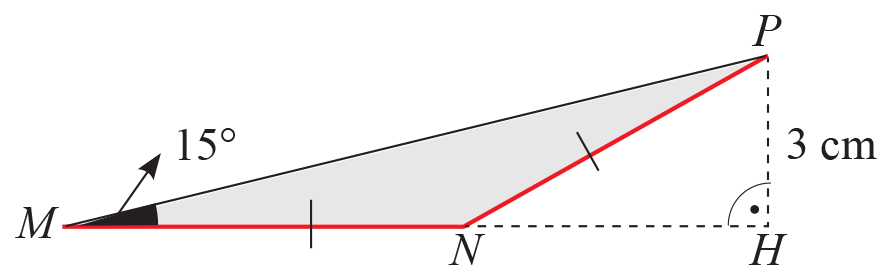
На чертежа ∆MNP (MN = NP) е равнобедрен и ∢NMP = 15°. Ако височината PH = 3 cm, намерете дължината на MN и лицето на ∆MNP.

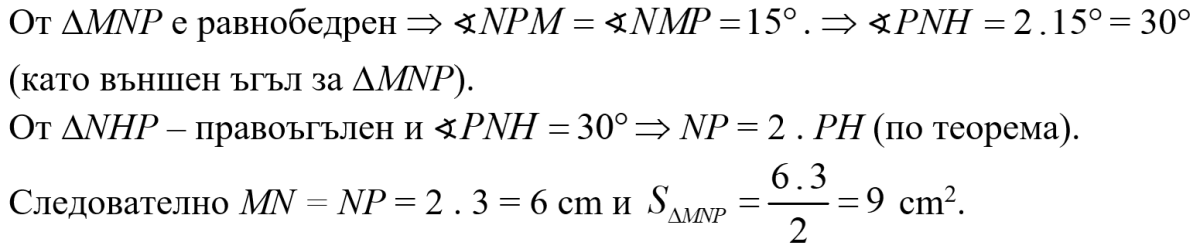
Даден е правоъгълен ∆ABC с хипотенуза AB и остри ъгли ∢BAC = α и ∢ABC = β.
Ако AB = 13 cm и BC = 6,5 cm, то α = 30° и β = 60°.
Ако AB = 2b cm и AC = b cm, то α = 60° и β = 30°.
Ако AB – BC = 8,1 cm и BC = 8,1 cm, то α = 30° и β = 60°.
На чертежа ∆ABC (∢BAC > 90°) е равнобедрен и AC = 14 cm. Ако височината BQ = 7 cm, намерете ∢ABC.
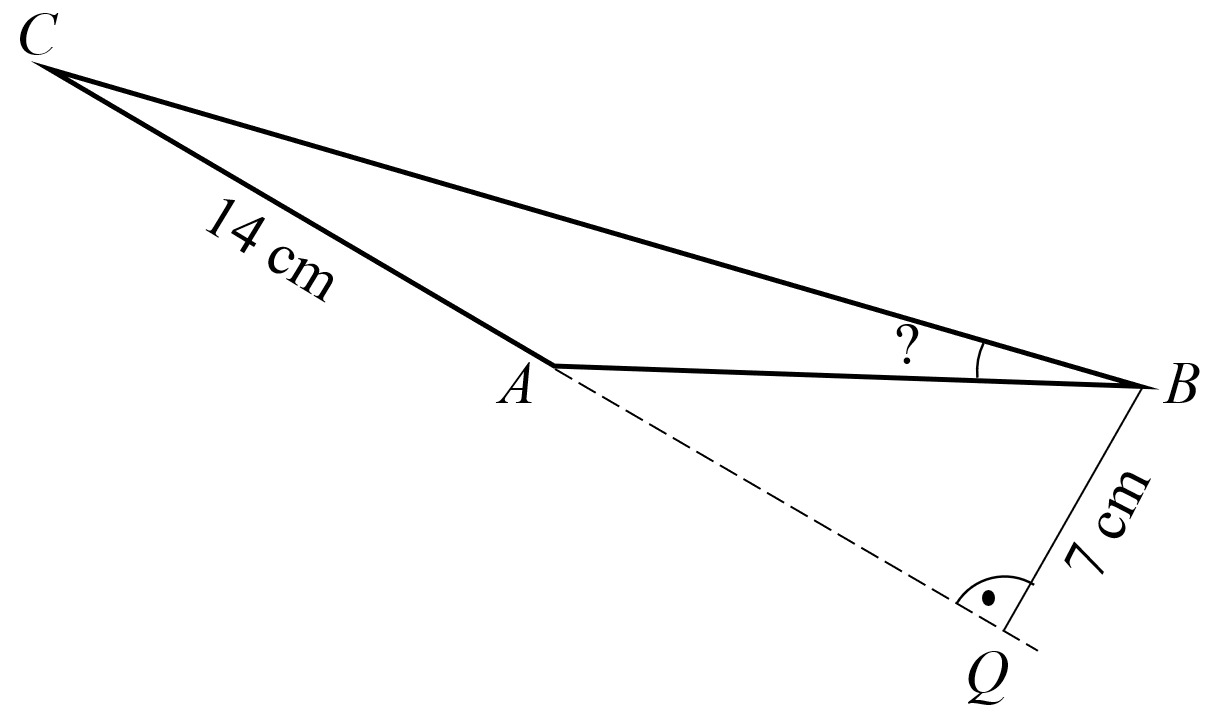

От ∆ABC е равнобедрен ⇒ AC = AB = 14 cm.
От ∆AQB – правоъгълен и хипотенузата AB = 2BQ ⇒ ∢QAB = 30°
(по теорема). От ∆ABC – равнобедрен ⇒ ∢ACB = ∢ABC. Но ∢QAB = 30° е външен ъгъл за ∆ABC ⇒ ∢ACB + ∢ABC = ∢QAB = 30° ⇒ ∢ACB = ∢ABC = 15°
(по теорема). От ∆ABC – равнобедрен ⇒ ∢ACB = ∢ABC. Но ∢QAB = 30° е външен ъгъл за ∆ABC ⇒ ∢ACB + ∢ABC = ∢QAB = 30° ⇒ ∢ACB = ∢ABC = 15°
Този час научих