Разлагане на многочлени на множители чрез изнасяне на общ множител
В този урок ще научите:
- какво означава да се разложи многочлен на множители;
- как да разлагате многочлен на множители чрез изнасяне на общ множител.
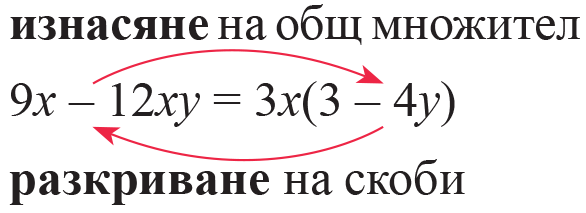
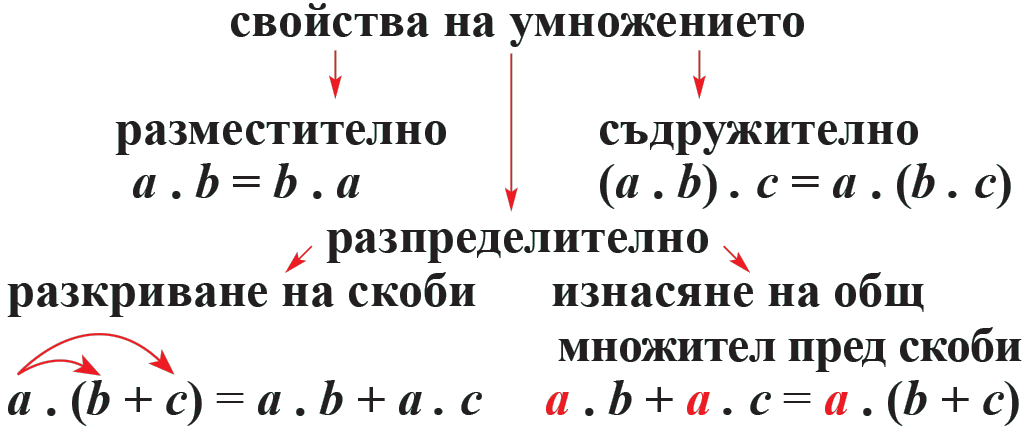
Представете като произведение.
• Числата 6 и 30 6 = 2 . 3; 30 = 2 . 15 = 2 . 3 . 5 Казваме, че числата 6 и 30 са разложени на прости множители. • Многочлените 5a + 5b и 2xyz – 3xyt 5a + 5b = 5(a + b) 2xyz – 3xyt = xy(2z – 3t) Използвахме разпределителното свойство на умножението. Казваме, че многочлените 5a + 5b и 2xyz – 3xyt са разложени на множители.
Важно!
Представянето на многочлен чрез тъждествено равно на него произведение наричаме разлагане на многочлена на множители.
Важно!
Когато за разлагане на многочлен на множители прилагаме разпределителното свойство на умножението, казваме, че разлагаме чрез изнасяне на общ множител.
Разгледайте таблицата със стъпките за разлагане на многочлена 12ax3y4 + 18ax2y6 чрез изнасяне на общ множител.

Изнесете общия множител извън скоби.
НОД (15, 20) = 5
15ax² – 20ax³y = 5ax²(3 – 4xy)
3m³n⁴ + m²n⁶ = m²n⁴(3m + n²)
НОД (3, 6, 12) = 3
3y² – 6y + 12y⁵ = 3y(y – 2 + 4y⁴)
НОД (36, 24, 12) = 12
36x²y – 24x³y⁴ – 12x² = 12x²(3y – 2xy⁴ – 1)
Разложете многочлена на множители.
(3a – 4)(5a + 2) – (3a – 4)²
(3a – 4)(5a + 2) – (3a – 4)²
= (3a – 4)(5a + 2 – (3a – 4))
= (3a – 4)(5a + 2 – 3a + 4)
= (3a – 4)(2a + 6)
x²(x – 3)² – x(x – 3)⁴
x²(x – 3)² + x(x – 3)⁴
= x(x – 3)² (x + (x – 3)²)
= x(x – 3)² (x + x² – 6x + 9)
= x(x – 3)² (x² – 5x + 9)
Разложете многочлена на множители.
x²(x – y) + 2(y – x)
Членовете в многочлените (x – y) и (y – x) имат противоположни коефициенти.
За да получим общ множител, от многочлена
(y – x) изнасяме пред скоби множител –1 (знака „–“). x²(x – y) + 2(y – x) = x²(x – y) + 2 . (–1)(x – y) = x²(x – y) – 2(x – y) = (x – y)(x² – 2)
(y – x) изнасяме пред скоби множител –1 (знака „–“). x²(x – y) + 2(y – x) = x²(x – y) + 2 . (–1)(x – y) = x²(x – y) – 2(x – y) = (x – y)(x² – 2)
m(m + n) – (–m – n)
m(m + n) – (–m – n)
= m(m + n) + (m + n)
= (m + n)(m +1)
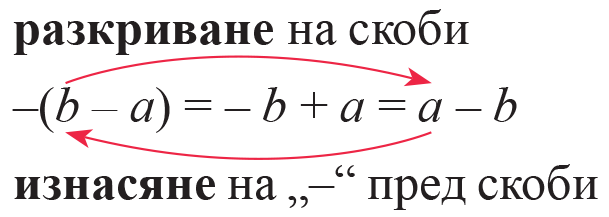
Представете като произведение.
a(2a – 1) – 2a + 1
От многочлена – 2a + 1 изнасяме пред скоби знака „–“ и получаваме:
a(2a – 1) – 2a +1
= a(2a – 1) – (2a – 1)
= (2a – 1)( a – 1)
= a(2a – 1) – (2a – 1)
= (2a – 1)( a – 1)
(2x – 4)(x +3) – x – 3
От многочлена – x – 3 изнасяме пред скоби знака „–“ и получаваме:
(2x – 4)(x +3) – x – 3
= (2x – 4)(x +3) – (x + 3)
= (x + 3)(2x – 4 – 1)
= (x + 3)(2x – 5)
= (2x – 4)(x +3) – (x + 3)
= (x + 3)(2x – 4 – 1)
= (x + 3)(2x – 5)
Представете като произведение.
(a – b)x² – 3(a – b)x + a – b
(a – b)x² – 3(a – b)x + a – b
= (a – b)x² – 3(a – b)x + (a – b)
= (a – b)(x² – 3x + 1)
4x(5y + 7) – 5y – 7
– 5y + 4x(5y + 7) – 7
= 4x(5y + 7) – 5y – 7
= 4x(5y + 7) – (5y + 7)
= 4x(5y + 7)(4x – 1)
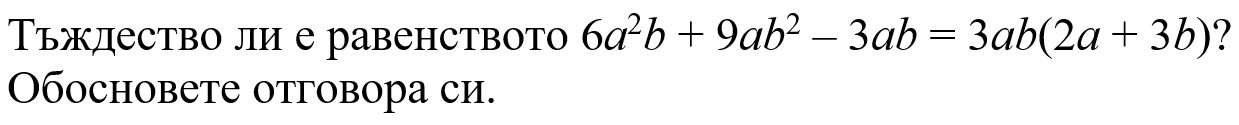
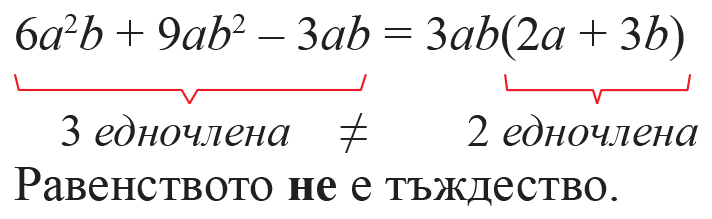
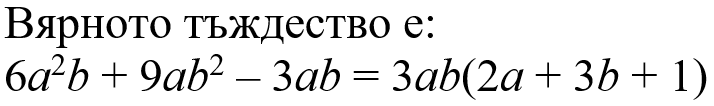
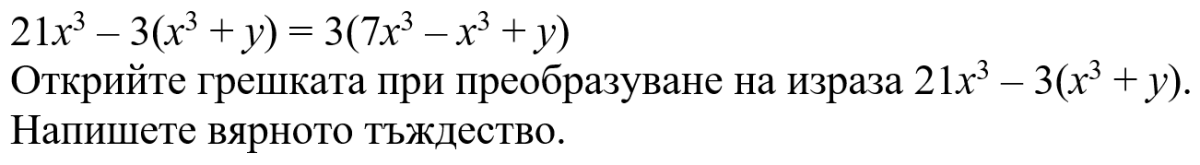
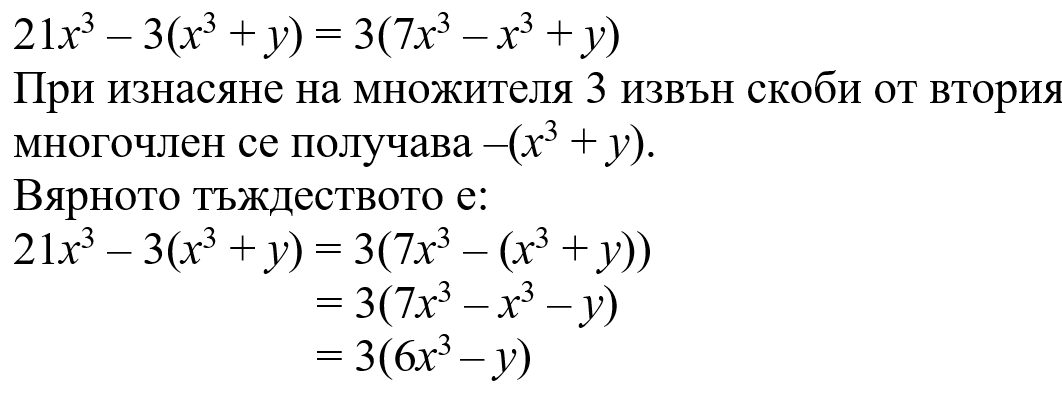
Този час научихме
