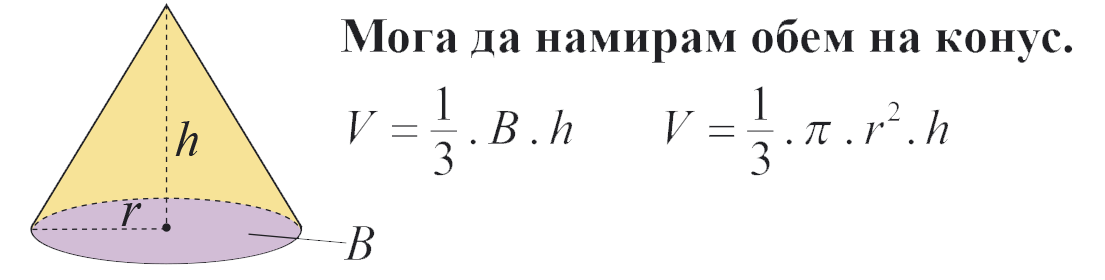Обем на прав кръгов конус
В този урок ще научите:
- формула за обема V на прав кръгов конус;
- да намирате обем на прав кръгов конус по дадени негови основни елементи;
- да намирате елементи на прав кръгов конус чрез формулата за обем.
Разгледайте начертаните 6-ъгълна и 12-ъгълна правилни пирамиди. Какво забелязвате?
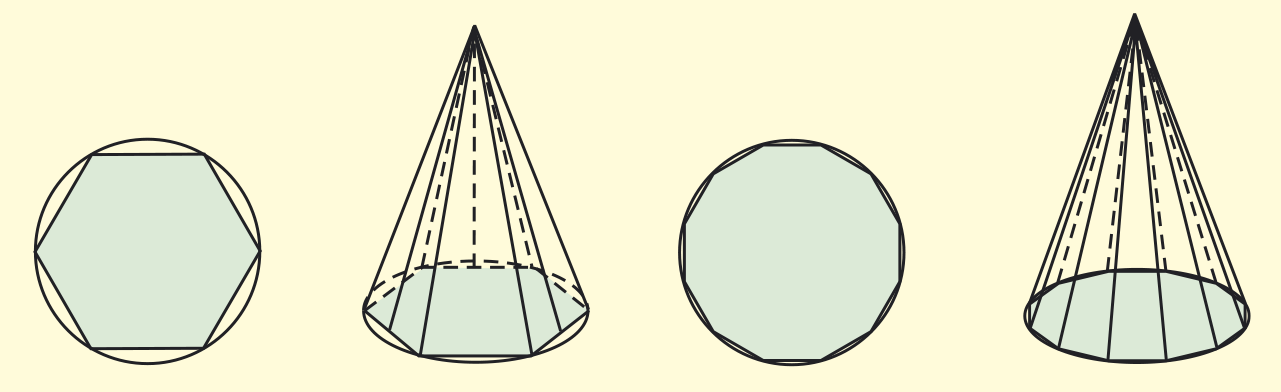
С увеличаване на броя на основните ръбове на пирамидата: • основите им все повече се доближават до кръг; • околните им ръбове се приближават един до друг и околните им повърхнини се доближават до коничната; • ако начертаем правилна 24-ъгълна и 48-ъгълна пирамида, те почти няма да се различават по форма от конус;
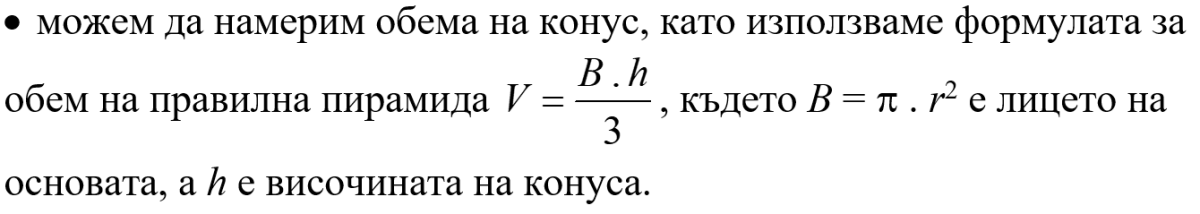
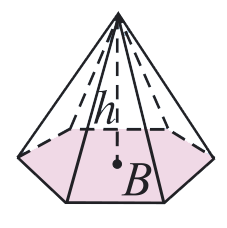
Формула за обем
на правилна пирамида и прав кръгов конус

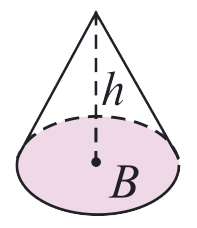

Експеримент
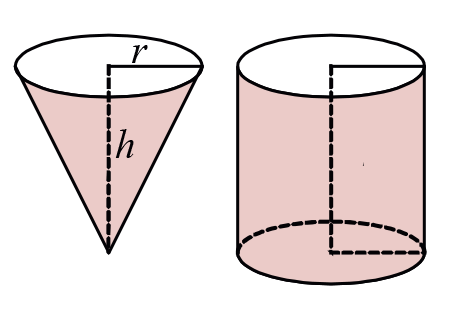
1. Направете конус без основа и цилиндър без горна основа, които са с равни дължини на диаметри и височини.
2. Напълнете с ориз или пясък конуса и след това го пресипете в цилиндъра.
3. Повторете процедурата, докато напълните цилиндъра.
4. Сравнете обемите на двете тела.
5. Какъв е изводът?
Като използвате калкулатор, намерете обема на конус с радиус на основата r, диаметър d и височина h. Използвайте, че π = 3,14.
Ако r = 3 dm и h = 8 dm, то V = 75,36 dm3.
Ако r = 10 cm и h = 6 cm, то V = 628 cm3.
Ако лицето на основата му е 50,24 cm2 и h = 24 cm, то V = 401,92 cm3.
Ако d = 60 cm и h = 1 m, то V = 94,2 L.
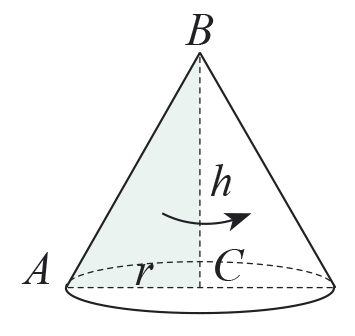
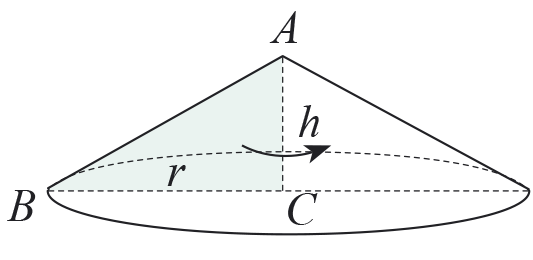
Даден е правоъгълен триъгълник ABC
с катети AC = 4 cm и BC = 6 cm.
Намерете обема на конусите, получени при завъртане на дадения триъгълник около единия и около другия му катет. Вярно ли е, че по-голям обем има конусът, получен при завъртане на ΔABC около по-малкия катет?
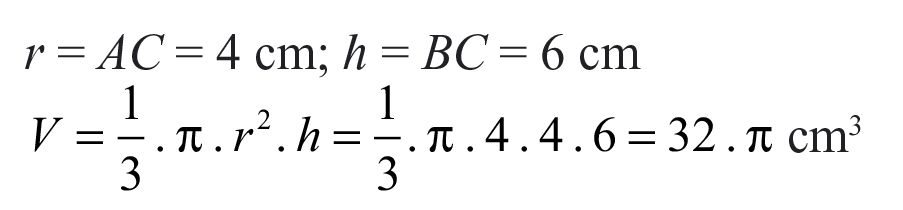
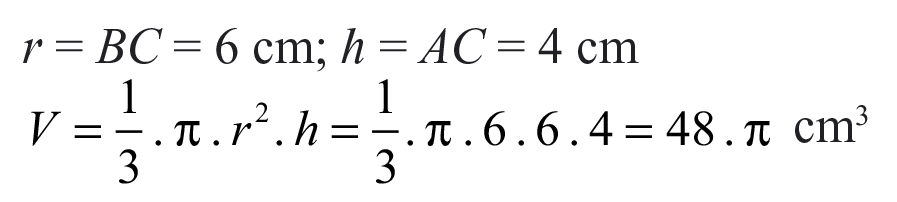
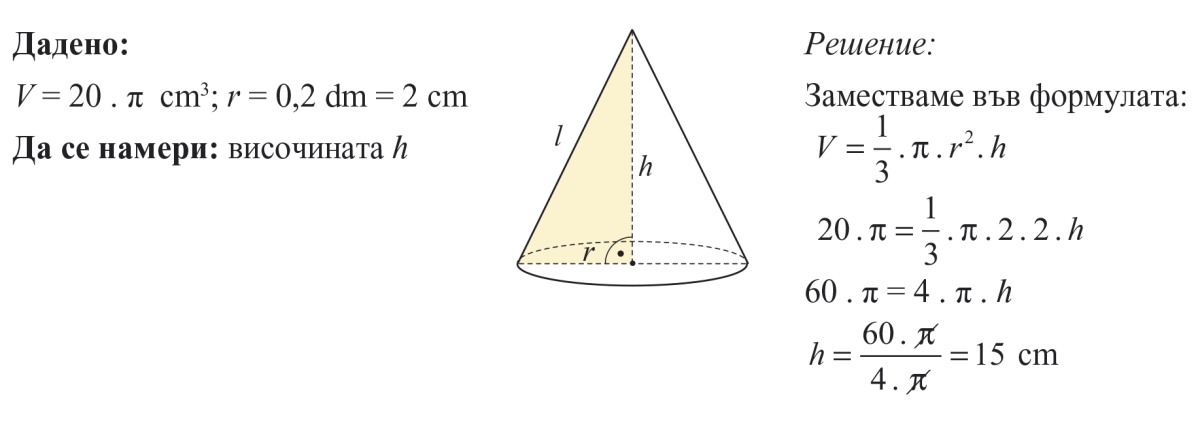
Обемът на конус е 20 . π cm3. Намерете височината му, ако радиусът му е 0,2 dm.
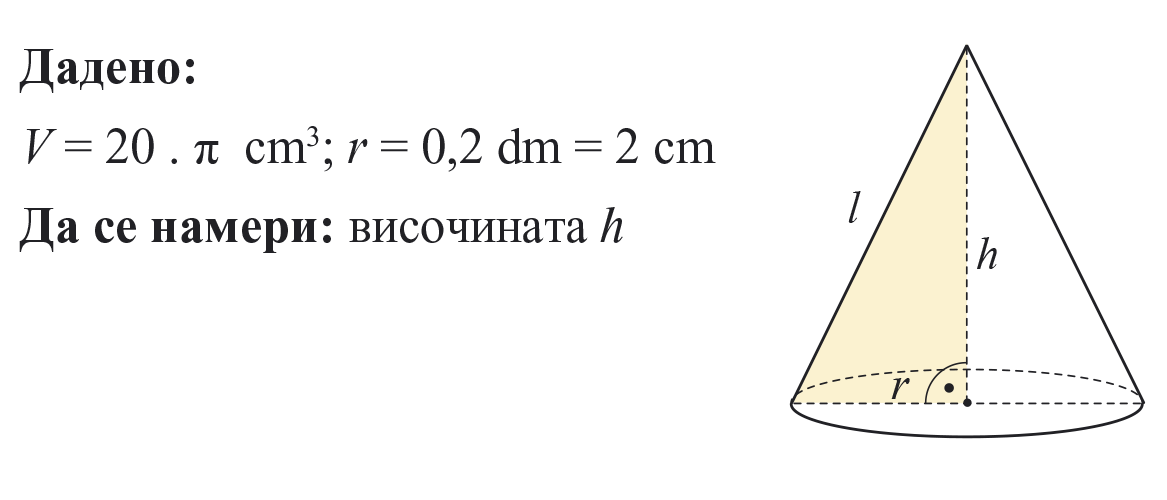
Този час научих